Infinity

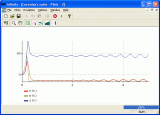Infinity is an innovative non-linear math application that allows you use complex mathematical expressions within equations to describe the problem which requires solution. It offers an unbeatable level of precision outperforming any competing math software when it comes to high-precision calculations. With it you can see the result immediately with the model is described using common math language.

It has a visually rich graphical engine calculating and intuitive user-friendly interface which are easy and useful. It's very useful to a lot of people such as Scientists, Engineers, Mathematicians, Business analysts,etc. So, why waste time? Go ahead and download free trial version now!

Download Now 2.0 MB         Buy Now $299.00 USD

Software Information		System Requirements
Version:	1.3.1	Windows 7/Vista/NT/2000/XP CPU: Pentium-233 MHz or highe 512 MB RAM 100 MB free disk space
File Size:	2.0 MB
License:	Free to try, $299.00 to buy
Screenshot :	View Screenshot
Rating :

• Scientists (biology, chemistry, physics, economics, business, IT) – model complex processes easy!
• Engineers – analyze prognostic reports, build more reliable hardware
• Mathematicians – make calculations easier!
• Business analysts – predict market fluctuations, stock and exchange rates, optimize business processes basing on future-paced modeling.

• The interface
1. allows to choose what data to show without repeating the calculation procedure;
2. allows to make scaling of the received results (in graphs) without repeating the calculation procedure;
3. allows to choose whether to display only the approximate solution or both the approximate solution and the area containing the exact solution (the degree of the distance between the exact and approximate solutions);
4. displays the dynamics of the calculation step change;
• Planned
1. the x1 (x2 (t)) phase trajectories construction;
2. the selected class systems calculation on the basis of transition to a new independent variable (instead of the variable t, the f(t) function is chosen as independent);
3. an opportunity of system parameters setting on each calculation step;
4. parametrical synthesis of the selected class system models;
• The kernel
1. the process of the found approximate solution removing from the unknown exact one is controlled (finds not only the approximate solution but also the area containing the exact solution);
2. the calculation step choice procedure is adaptive and anticipates the dynamics of the solution change;
3. allows to overcome correctly the first and the second kinds discontinuities in the solution;
4. allows to compute ordinary nonlinear non-autonomous systems of differential equations with the limiting absolute local error top level given;
5. provides an opportunity to choose between a more exact solution from the approximate one or between a faster calculation;
6. reveals locally unstable areas in the solution;
7. no necessity to bring the initial equations system to the normal Cauchy form;
• Main features:
1. Solving ordinary differential equations systems;
2. Solving ordinary differential equations (ODE);
3. Solving nonlinear non-stationary differential equations;
4. Solving ordinary nonautonomous differential equations systems;
5. Solving linear algebraic equations systems;
6. Work with polynoms: open the brackets and expression normalization, etc.
7. Solving nonlinear non-stationary differential equations systems;
8. Solving derivatives;